أسباب تسرب المياه من الثلاجة

عندما نسمع بكلمة رقم ( Number ) يفكر معظمنا بنظام الأرقام العشرية Decimal Nurnbers المألوفة والمكونة من الأرقام العشرية الأولية ( 0,1,2,3,4,5,6,7,8,9) حيث أن نظام العد الشائع الاستعمال هو استخدام عشرة ارقام من الصفر الى التسعة ويطلق عليه النظام العشري لأنه يحتوي على عشرة ارقام، وهناك أنظمة أخرى (أنظمة العد في الحاسوب) لا يعرفها إلا الذين يختصون بدراسة علم الإلكترونيك والحاسبات والاتصالات ومنها الاعداد الثنائية Binary Numbers والاعداد الثمانية Octal Numbers والاعداد السادسة عشرة Hexadecirnal Nutnbers.

 الأنظمة العددية Numbering System

سنتعرف فيما يلي على  الأنظمة العددية Numbering System بشكل مبسط وميسر.

جدول الأنظمة العددية

انواع الأنظمة العددية

تتمثل أنواع الأنظمة العددية فيما يلي:

1. نظام العد العشري Decimal System
2. نظام العد الثنائي Binary System
3. نظام العد الثماني Octal System
4. نظام العد السادس عشر Hexadecimal System

نظام العد العشري Decimal System

يعد هذا النظام من أكثر الأنظمة انتشارا ومناسب للإنسان، ففي الحياة الطبيعية يستعمل الإنسان النظام العشري في العمليات الحسابية المختلفة .

سمى النظام العشري بهذا الاسم هذا لأنه يتكون من عشرة أرقام (2,1,0...9).

تعتمد قيمة الرقم على موقعه في العدد العشري؛ أي إن قيمة الرقم الحقيقية تعتمد على قيمته المنزلية، وهذا يعني أن الرقم قد يأخذ أكثر من قيمة، وأن موضعه داخل العدد يحدد قيمة ذلك الرقم تزداد قيمة الرقم إذا حرك نحو اليسار ، وتقل قيمته إذا حرك في اتجاه اليمين. وبناء على ذلك فإن الرقم الذي يقع أقصى يمين العدد هو الأصغر منزلة (Least Significant Bit: LSB) والرقم الذي يقع أقصى يسار العدد هو الأكبر منزلة (Most Significant Bit: MSB).

يعد النظام العشري من أنظمة العد الموضعية (Local CountingSystems)؛ إذ تعتمد فيه قيمة الرقم على موقعه في العدد العشري.
ويمكن حساب الرقم على أساس ما يعرف بمرتبة العدد؛ ويمكن التعبير عن الرقم باستعمال الأساس 10 مرفوعا إليه الأس بحيث يبدا (2,1,0...).

مثال الرقم 354

354 = 4 أحاد + 5 عشرات + 3 مئات

      = 4 + 100х3+ 10х5

      = 4 10 ²х3+10 ¹х5+10 ⁰х

      = 4 + 50 + 300 = (354)₁₀

ملاحظة

يمكن معرفة إلى أي نظام ينتمي هذا الرقم من خلال الرقم الذي يكتب تحت الأقواس المحيطة بالرقم مثلا (354)₁₀ يدل على أن هذا الرقم ينتمي إلى النظام العشري أما الرقم(354)2 فينتمي إلى النظام الثنائي والرقم (354)8 ينتمي إلى النظام الثماني والرقم (354)16 ينتمي إلى النظام السادس عشر .

نظام العد الثنائي Binary System (الأنظمة العددية في الحاسوب)

هو النظام الذي تفهمه الآلة و يتكون من رقمين وهما 0 ,1 ويسمى كل حد منهما الحد الثنائي (Bit)؛ ويستخدم في الدوائر الإلكترونية وفي التصميم الداخلي للحاسوب حيث يتم إعطاء قيمة صفر عندما يكون الجهد مساويا للصفر بينما يعطى الرقم 1 إذا كان الجهد مساويا (5V+).
وهناك العديد من الأجهزة والمعدات الرقمية التي تستخدم النظام الثنائي وهو من أكثر الأنظمة ملاءمة للاستخدام في الأجهزة الرقمية؛ لأن لجميع البوابات والدارات المنطقية مخارج ثنائية الحالة فالتيار الكهربائي إما أن يمر بالدارة وإما ألا يمر وكذلك الحال بالنسبة إلى المفاتيح الكهربائية فإما أن يكون المفتاح مغلقا (ON) وإما أن يكون مفتوحا (OFF) ويمكن استخدام الرقم (0) للتعبير عن حالة المفتاح المفتوح والرقم (1 ) للتعبير عن حالة المفتاح المغلق.
ويمكن التعبير عن الرقم في النظام الثنائي باستعمال الأساس 2 مرفوعا إليه الأس حسب المرتبة بحيث يبدا 2,1,0... ويمكن تمثيلها كالتالي :

2 ⁰ = 1
2 ¹ = 2
2 ² = 4
2 ³ = 8

الصفر على الشمال في النظام الثنائي مثله مثل الصفر على الشمال في النظام العشري ليس له قيمة لذلك نجد التالي:

11001=011001=0011001=00011001

ولأن النظام الثنائي يحتوي فقط على رقمين (0) و(1 )؛ فإن تمثيل الحالات الثنائية داخل الأجهزة الرقمية يكون أكثر سهولة باستخدام هذا النظام يسمى كلا الرقمين (0) و(1) رقما ثنائيا واختصاره (bit).
لتمثيل كل رقم ثنائي يلزم توافر خانة وأحدة فقط؛ لذا أصبح شائعا إطلاق اسم (بت) على الخانة المخصصة للرقم في العدد الثنائي.

الفرق بين Bit و Nibble و Byte

الفرق بين Bit و Nibble و Byte

كل خانة من خانة النظام الثنائي يطلق عليها Bit، وكل أربع خانات يطلق عليها Nibble، وكل 8 خانات يطلق عليها Byte.

 

نظام العد الثماني Octal System

 

يتكون النظام الثماني من 8 أرقام (7 ..0) ويستخدم هذا النظام في كتابة بعض البرامج الخاصة؛ لأنها لو كتبت بالنظام الثنائي لأدى ذلك إلى حدوث العديد من المشاكل بسبب كثرة (0 ,1)، يشبه النظام الثماني النظام العشري في أول ثمانية أرقام (7..0) ويختلف عنه في كونه أن الرقمين 9 ، 8 لا يمكن استخدامهما في النظام الثماني .

 يمكن التعبير عن الرقم كما في الأنظمة الأخرى بطريقة الأساس 8 والاس (2,1,0...) كالتالي: 

8 ⁰ = 1
8 ¹ = 8
8 ²  = 64
8 ³ = 512

نظام العد السادس عشر Hexadecimal System

هو نظام وسطي بين النظام العشري ونظام الثنائي وهو مناسب للآلة ويتميز هذا النظام بسهولة التعبير عن القيم الكبيرة والصغيرة بدلا من النظام الثنائي حيث أن كل حد في النظام الثنائي يقابله أربعة حدود في النظام السادس عشر كالتالي:

16 ⁰ = 1
16 ¹ = 16
16 ² = 256
16 ³ = 4096

ملاحظة

يتكون نظام العد السادس عشر من الأعداد العشرية مضافا إليه الحروف(A-B-C-D-E-F) كبديل للأعداد 10,11,12,13,14,15.

كيفية التحويل بين الأنظمة العددية

سوف نتعرف من خلال السطور القادمة على كيفية التحويل بين الأنظمة العددية المختلفة.

التحويل من النظام الثنائي Binary إلى النظام العشري Decimal

للتحويل من النظام الثنائي إلى النظام العشري يتم ضرب كل رقم من أرقام العدد في وزن الخانة الموجود فيها ثم جمع هذه المضاريب و نحصل على الرقم العشري.

مثال للتوضيح

(101)₂ = 1 × 2⁰ + 0 × 2¹ + 1 × 2²

       = 1 × 1 + 0 × 2 + 1 × 4

       = 1 + 0 + 4

       = 5

(101)₂ = (5)₁₀

مثال أخر

التحويل من النظام العشري Decimal إلى النظام الثنائي Binary

يتم التحويل من النظام العشري إلى النظام الثنائي بطريقة باقي القسمة حيث يقسم العدد على (٢) ونستمر في عملية القسمة إلى أن يصل ناتج القسمة إلى صفر عندها تكون انتهت القسمة ونقرا باقي القسمة من الأسفل إلى الأعلى وتكتب من اليسار إلى اليمين كالتالي:

مثال حول الرقم العشري(64)₁₀ إلى النظام الثنائي

(64)₁₀= (1000000)₂

طريقة أخرى للتحويل من النظام العشري إلى النظام الثنائي

نبحث عن أرقام مجموعها يساوي العدد العشري المطلوب.

التحويل من النظام العشري Decimal إلى النظام السادس عشر Hexadecimal

يمكن التحويل من النظام العشري إلى النظام السداسي عشر عن طريق إستخدام الاله تجنبا لحدوث الخطأ.

التحويل من النظام السادس عشرHexadecimal إلى النظام العشري Decimal

يكون الاساس لدينا هو 16 مرفوع لأس الخانة الموجود بها  ثم جمع هذه المضاريب و نحصل على الرقم العشري كالتالي:

التحويل من النظام الثنائي Binary إلى النظام السادس عشر Hexadecimal

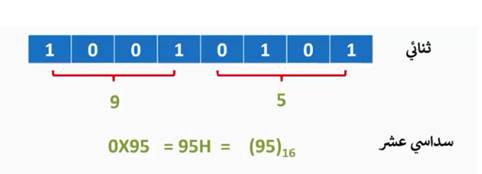
للتحويل من النظام الثنائي إلى النظام السادس عشر نعد كل أربعة أرقام (خانات) Nibble تمثل رقما (خانة واحدة) في النظام السادس عشر بحيث نبدأ من المرتبة الأقل أهمية (LSB) .

حول الرقم  (011011110011)₂ إلى النظام السادس عشر.

(011011110011)₂

     ⬇️       ⬇️       ⬇️

    3              6

(011011110011)₂ = (6F3)₁₆

مثال أخر

التحويل من النظام السادس عشر Hexadecimal إلى النظام الثنائي Binary

للتحويل من النظام السادس عشر إلى النظام الثنائي نعد كل رقم في النظام السادس عشر يمثل أربعة أرقام (خانات) Nibble في النظام الثنائي .

مثال ذلك حول الرقم (1000)₁₆ من النظام السادس عشر إلى النظام الثنائي

(1000)₁₆

(0        0       0        1)  ₁₆

  ⬇️       ⬇️       ⬇️        ⬇️ 

_{0000  0000  0000   0001}

(1000)₁₆= (0000 0000 0000 0001) ₂

                 = (1000000000000)₂

مثال أخر

الجمع البسيط للأعداد الثنائية

0+0=0
0+1=1
0+1=1
1+1=10 حيث أن مجموع 1+1 هو 2 في النظام العشري ولكن نحن هنا نجمع تبعا للنظام الثنائي فتم كتابة رقم 2 بالشكل التالي 10.

الأرقام السالبة في النظام الثنائي

يتم كتابة الارقام السالبة في النظام الثنائي بثلاث طرق هي:

نظام مقدار الإشارة Signe magnitude

نظام مقدار الإشارة Signe magnitude

في هذا النظام نقوم بحجز أخر(Bit) على اليسار ليعبر عن الإشارة فيكون 0 لو موجب، ويكون 1 لو سالب، ولكن يعيب هذه الطريقة أنها تخزن الصفر مرة على أساس موجب ومرة على أنه سالب.

نظام المتمم الأول First complement

نظام المتمم الأول First complement

في هذا النظام نقوم بحجز أخر(Bit) على اليسار ليعبر عن الإشارة فيكون 0 لو موجب، ويكون 1 لو سالب، ثم نعكس كل البتات الباقية، ويعيب على هذه الطريقة وجود طريقتان مختلفتان تماما لتخزين الصفر.

نظام المتمم الثاني Second complement

نظام المتمم الثاني Second complement

في هذا النظام نقوم بحجز أخر(Bit) على اليسار ليعبر عن الإشارة فيكون 0 لو موجب، ويكون 1 لو سالب، ثم نعكس كل البتات المتبقية ثم نضيف إليها واحد (1).

أسئلة شائعة

لماذا يستخدم الحاسوب النظام الثنائي؟

السبب الرئيسي لاستخدام نظام الأرقام الثنائية في الحوسبة هو أنه بسيط. لا تفهم أجهزة الكمبيوتر اللغة أو الأرقام بنفس الطريقة التي نفهمها. كل ما لديهم بالفعل للعمل به هو المفاتيح والإشارات الكهربائية، سواء في وضع التشغيل أو الإيقاف. لتشفير التعليمات أو تخزين القيم باستخدام المفاتيح - والتي يمكن أن تكون إما متوقفة عن العمل أو قيد التشغيل فقط - فإن النظام الثنائي هو الخيار المناسب.
في الكود الثنائي، يتم تمثيل "off" بالرقم 0، ويتم تمثيل "on" بالرقم 1. تستخدم أجهزة الكمبيوتر الترانزستورات لتكون بمثابة مفاتيح إلكترونية.
يتم استخدام نظام الترقيم الثنائي لترميز كل شيء بدءًا من الذاكرة وحتى الصور التي تظهر على الشاشة. وبالتالي فهو الأساس لتخزين ونقل البيانات في معظم الأجهزة الإلكترونية الرقمية.

ما هو أساس النظام العشري؟

النظام العشري هو الذي يستخدم الرقم 10 كأساس ويتطلب 10 أرقام مختلفة، الأرقام 0، 1، 2، 3، 4، 5، 6، 7، 8، 9. ويتطلب أيضًا نقطة (فاصلة عشرية). لتمثيل الكسور العشرية. وتسمى طريقة الإشارة إلى الأرقام العشرية بالأساس 10 أيضًا بالتدوين العشري.



مراجع
دورة الإلكترونيات الرقمية : أنظمة العد الرقمية.
مناهج التعليم العراقي.
مصادر أخرى